Text erkannt:
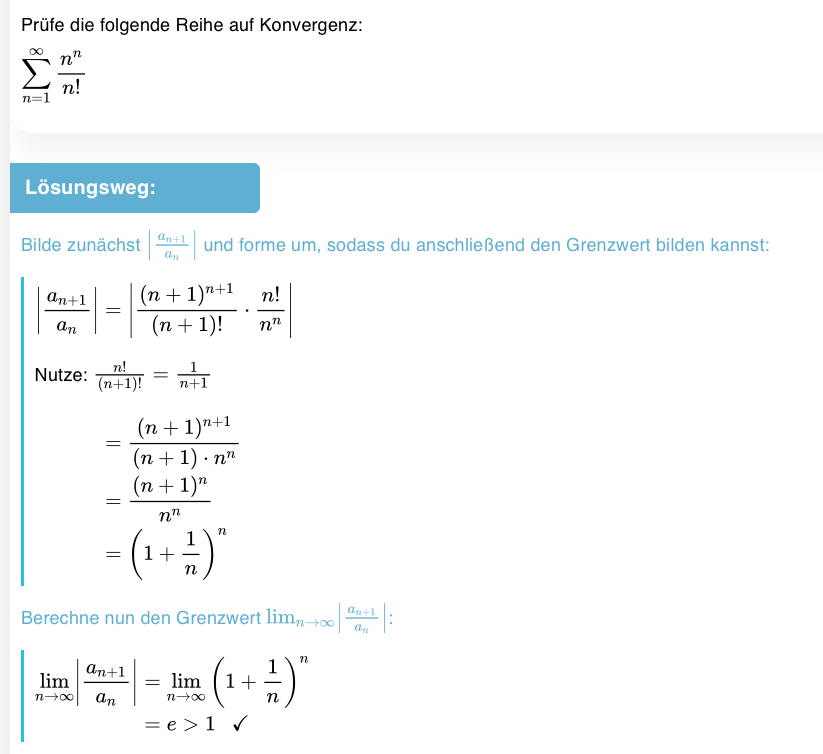
Prüfe die folgende Reihe auf Konvergenz:
\( \sum \limits_{n=1}^{\infty} \frac{n^{n}}{n !} \)
Lösungsweg:
Bilde zunächst \( \left|\frac{a_{n+1}}{a_{n}}\right| \) und forme um, sodass du anschließend den Grenzwert bilden kannst:
\( \begin{array}{l} \left|\frac{a_{n+1}}{a_{n}}\right|=\left|\frac{(n+1)^{n+1}}{(n+1) !} \cdot \frac{n !}{n^{n}}\right| \\ \text { Nutze: } \frac{n !}{(n+1) !}=\frac{1}{n+1} \\ =\frac{(n+1)^{n+1}}{(n+1) \cdot n^{n}} \\ =\frac{(n+1)^{n}}{n^{n}} \\ =\left(1+\frac{1}{n}\right)^{n} \\ \end{array} \)
Berechne nun den Grenzwert \( \lim \limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|: \)
\( \begin{aligned} \lim \limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right| & =\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n} \\ & =e>1 \end{aligned} \)
Hallo, ich würde gerne wissen, wie man hier umgestellt hat: Die erste Zeile ergibt für mich absolut Sinn, da man hier nur das Quotientenkriterium angewendet hat, aber was passiert danach? Ich dachte zuerst, dass da einfach das Fakultät gekürzt wird, aber dann müsste ja das n im Zähler noch stehen, aber da steht nun eine 1. Ich danke im Voraus für einen kurzen Input! :)