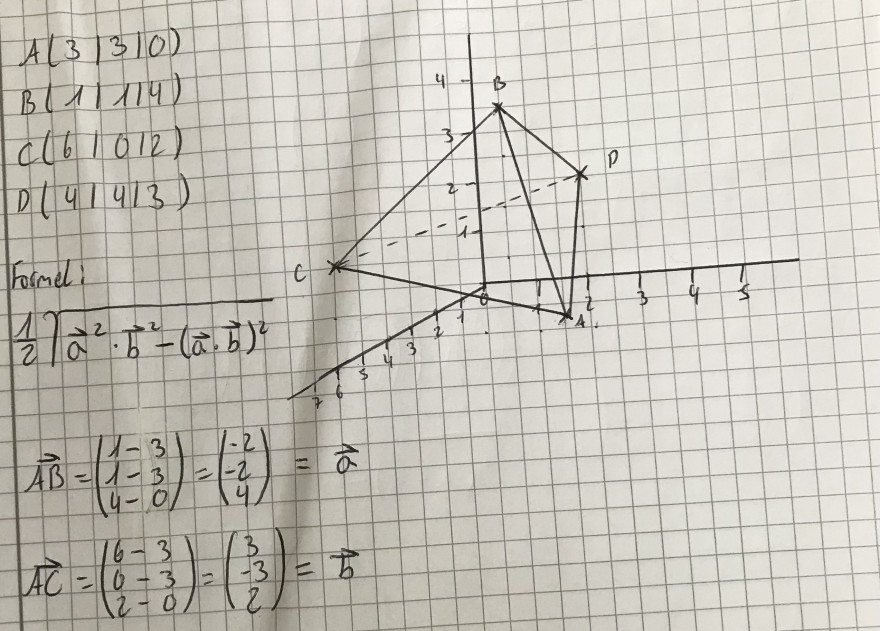
Aufgabe: Oberfläche einer Pyramide
Bestimmen Sie den Oberflächeninhalt der Pyramide mit den Eckpunkten A(3|3|0), B(1|1|4), C(6|0|2), D(4|4|3).
Problem/Ansatz:
Hey ich bräuchte Hilfe bei dieser Aufgabe. Ich habe schon die Vektoren AB (-2|-2|4) und AC(3|-3|2) ausgerechnet für die Seite ABC. Wir müssen mit der Formel rechnen die unten im Bild angegeben ist und ich verstehe nicht wie ich die Zahlen einsetzen soll. AB ist bei mir der Vektor a und AC der Vektor b. Anscheinen soll das Ergebnis ungefähr 10,77 für die Seite ABC sein aber egal wie ich die Zahlen einsetze kommt bei mir immer etwas komplett anderes raus. Könnte vielleicht jemand mir die Seite ABC vorrechnen damit ich alle anderen Seiten selbst berechnen kann? Ich bräuchte wirklich ein Beispiel an dem ich mich bei meinen zukünftigen Berechnungen orientieren kann.