Im Jahr 2020 sind
3 441 000 Pkw neu zugelassen worden. Davon entfielen 35,6 % auf private Zulassungen , die übrigen auf gewerbliche Zulassungen,Von den neu zugelassenen Pkw hatten 25 000 einen Elektroantrieb. Von allen neu zugelassenen Elektroautos wurden 64,6 % gewerblich zugelassen.
Stelle die Situation in der folgenden Vierfeldertafel mit relativen
Häufigkeiten dar. Runde alle Werte auf drei Nachkommastellen.
Problem/Ansatz:
Ist meine Lösung richtig?
Text erkannt:
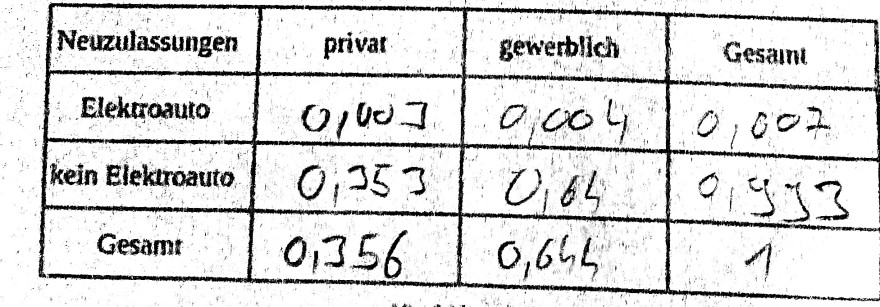
\begin{tabular}{|c|c|c|c|}
\hline Neuzulassungen & privar & gewerblich & Gesam \\
\hline Elekroauto & 0,007 & 0,004 & 0,007 \\
\hline kein Elekroauto & 0,353 & 0,64 & 0,933 \\
\hline Gesamt & 0,356 & 0,644 & 1 \\
\hline
\end{tabular}
