in
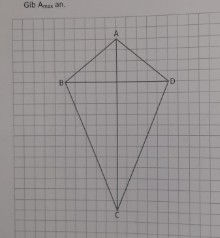
Verlängert man die \( 5 \mathrm{~cm} \) lange Diagonale \( \overline{\mathrm{BD}} \) eines Drachenvierecks \( A B C D \) über \( B \) und \( D \) hinaus um jeweils \( x \mathrm{~cm} \) und verkürzt gleichzeitig die \( 8 \mathrm{~cm} \) lange Diagonale \( \overline{\mathrm{AC}} \) von \( C \) aus um \( 0,5 \times \mathrm{cm} \), so entstehen neue Drachenvierecke \( A B_{n} C_{n} D_{n} \).
a) Zeichne das Drachenviereck für \( x=2 \) in die Zeichnung ein.
b) Welche Werte sind für \( x \) zulässig? Gib ein sinnvolles Intervall an.
c) Für welchen Wert von \( x \) entsteht eine Raute \( A B_{2} C_{2} D_{2} \) ?
d) Bestimme den Flächeninhalt der Drachenvierecke \( A B_{n} C_{n} D_{n} \) in Abhängigkeit von \( x \).
e) Für welchen Wert von \( x \) hat das Drachenviereck \( A B_{3} C_{3} D_{3} \) den größtmöglichen Flächerinhalt? Gib Amax an.