Aloha :)
Wir betrachten die Funktion$$f(x)=-x^3+3x+2$$Zuerst brauchen wir das Maximum und den Wendepunkt der Funktion.
Für deren Berechnung benötigen wir die Ableitungen:$$f'(x)=-3x^2+3=-3(x^2-1)=-3(x+1)(x-1)$$$$f''(x)=-6x$$$$f'''(x)=-6$$
Kandidaten für Extremstellen sind die Nullstellen der 1-ten Ableitung:$$x_1=-1\quad\text{und}\quad x_2=1$$Wir prüfen beide Kandidaten durch Einsetzen in die 2-te Ableitung:$$f''(x_1)=f''(-1)=6>0\implies\text{Minimum}$$$$f''(x_2)=f''(1)=-6<0\implies\text{Maximum}$$
Kandidaten für Wendepunkte sind die Nullstellen der 2-ten Ableitung: \(\quad x_w=0\).
Zur Prüfung setzen wir diesen Kandidaten in die 3-te Ableitung ein. Diese ist konstant gleich \((-6)\), also ungleich Null, sodass bei \(x_w=0\) tatsächlich ein Wendepunkt vorliegt.
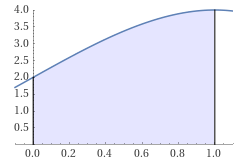
Schließlich können wir nun die Fläche unter dem Graphen von \(f(x)\) zwischen der x-Achse, dem Wendepunkt bei \(x_w=0\) und dem Maximum bei \(x_2=1\) bestimmen:$$F=\int\limits_{x_w}^{x_2}f(x)\,dx=\int\limits_0^1\left(-x^3+3x+2\right)dx=\left[-\frac{x^4}{4}+\frac{3x^2}{2}+2x\right]_0^1$$$$\phantom F=-\frac14+\frac32+2=\frac{-1}{4}+\frac{6}{4}+\frac{8}{4}=\frac{13}{4}=3,25$$