Hast du das Parabelstück mal geplottet?
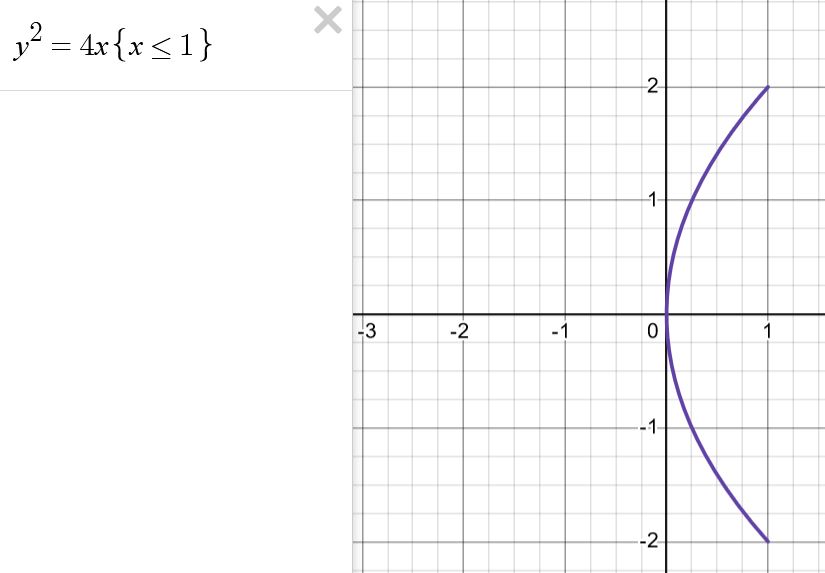
Du hast faktisch \( x \) als Funktion von \(y\) gegeben:
\(x=f(y) = \frac 14y^2\)
Damit ergibt sich auch sofort die Parametrisierung \(y=t\).
Du musst nur noch die folgende Ungleichung lösen:
\(x\leq 1 \Leftrightarrow \frac 14 y^2 \leq 1 \Leftrightarrow |y|\leq 2 \)
Damit gilt für deinen Parameter \(y=t \in [-2,2]\).
Den Rest kannst du ja, wie du sagtest.
Nachtrag wegen Kommentar:
Deine vorgegebene Parametrisierung ergibt sich, wenn du
statt \(y= t\) mit \(t\in[-2,2]\) einfach \(y=2t\) mit \(t\in [-1,1]\) nimmt.
Ist das wirklich so schwer?
