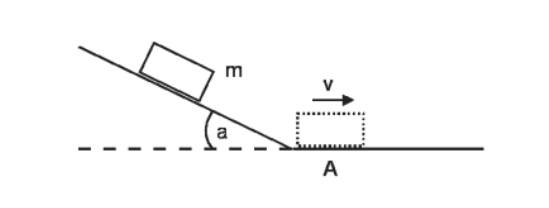
Ein Steinblock der Masse m = 150 kg rutscht eine schiefe Ebene hinunter (s. Skizze). Der Neigungswinkel sei α = 23° und der Gleitreibungskoeffizient zwischen Stein und Boden beträgt μG = 0,5
a) Zeichnen Sie alle auf den Stein wirkende Kräfte ein.
b) Berechnen Sie die resultierende Beschleunigung des Steins entlang einer schiefen Ebene.
c) Ab dem Punkt A ist die Rutschfläche flach (α = 0) und der Stein besitzt dort eine Geschwindigkeit von \(v= 3 m s^{-1}\). Wie lange dauert es, bis der Stein von der Reibungskraft bis zum Stillstand abgebremst wird? Wie weit rutscht er noch in dieser Zeit?
Meine Lösungen:
zu a)
FR Reibungskraft (N)
µ Reibungszahl
FN Normalkraft
FG Gewichtskraft
zu b)
Ansatz:
Ich habe folgende Formeln gefunden:
FR=µ*FN
FN=FG*cosα
F=m*a
FG=m*g
Auf jeden Fall sind gegeben:
μG=0,5
m=150 kg
α=23°
Lösungsversuch:
gesucht: a (Beschleunigung)
FG=m*g=150 kg*9,81N/kg=1471,5N
FN=FG*cosα=1471,5N*cos(23)=1354,52N
FR=µ*FN=0,5*1354,52N=677,10N
F=m*a
a=F/m=1354,52N/150N=9,03m/s
Die Werte scheinen zu hoch zu sein. Eigentlich müssten die Werte zwischen 60 und 80N liegen, oder ich irre mich.
zu c)
gesucht: t (Zeit in Sekunden)
Hier muss auf jeden Fall eine Formel umgestellt werden. Ich vermute das Ergebnis aus Teilaufgabe b), also die Beschleunigung und ein weiterer Faktor.
t=a*? oder t=a/?