Ich soll folgendes Gleichungssystem nach den unbekannten x,y auflösen.
$$I. ax+by=a^2+b^2$$$$II. −bx+ay=a^2+b^2 $$
zuerst habe ich versucht die beiden Gleichungen gleichzusetzen, da sie auf einer Seite gleich sind, da kam ich aber wieder auf die Zweite Gleichung.
deswegen bin ich folgendermaßen vorgegangen: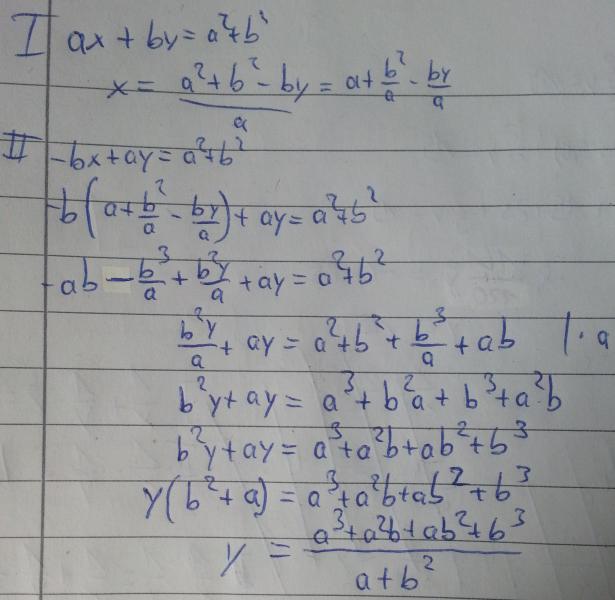
Ist meine Vorgehensweise bis hierhin korrekt oder habe ich etwas falsch gemacht?
und wie mache ich nun weiter? muss ich erst eine Polynomdivision durchführen? und wenn ja wie mache ich das hier?