Das Volumen V einer Pyramide errechnet sich aus dem Inhalt der Grundfläche (G) und der Höhe (h) gemäß
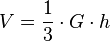
Diese Formel gilt für jede Pyramide. Es spielt also keine Rolle, ob die Grundfläche ein Dreieck, Viereck, Fünfeck, ... ist. Die Formel ist auch gültig, wenn der Höhenfußpunkt nicht mit dem Grundflächenmittelpunkt übereinstimmt oder die Grundfläche gar keinen Mittelpunkt besitzt. Im Spezialfall einer quadratischen Pyramide ergibt sich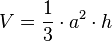 
, wobei a die Seitenlänge der quadratischen Grundfläche ist und h die Höhe.
Die allgemeine Formel 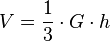entspricht übrigens der Volumenformel 
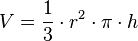für einen Kreiskegel. Dies liegt daran, dass jede Pyramide die Definition eines allgemeinen Kegels erfüllt. Umgekehrt kann ein Kegel auch als Pyramide mit einem regelmäßigen n-Eck als Grundfläche aufgefasst werden, das mit n → ∞ zu einem Kreis entartet ist.
Quelle: https://de.wikipedia.org/wiki/Pyramide_(Geometrie)
d.h. hier müsstest du zuerst die grundfläche berechnen,
$$h_c=\sqrt{a^2-\frac{1}{4}c^2}$$
$$h_c=\sqrt{(5,9cm)^2-\frac{1}{4}(9,3cm)^2}}$$
$$h_c=3,63cm$$
$$V=\frac{1}{3}(G\cdot h)$$
$$V=\frac{1}{3}(\frac{h_c \cdot c}{2}\cdot h)$$
$$V=\frac{1}{3}(\frac{3,63cm \cdot 9,3cm}{2}\cdot 9,8cm)$$
$$V=55,16cm^2$$
