Wir betrachten die Funktion f: R → R,
f(x) = (x-1)² / cos (pi/2 x) für x ≠ 1
f(x) = = 0, für x = 1
Jetzt muss man ja lim x −>1 (x-1)² / cos (pi/2 x)
Was du jetzt überprüft ist doch eigentlich die Stetigkeit
der Funktion.

Hier läßt sich zeigen das die Grenzwerte lim x −> 1 gleich 0 sind.
Die Funktion ist dort also stetig.
Die Funktion hat allerdings Polstellen und ist daher nicht stetig.
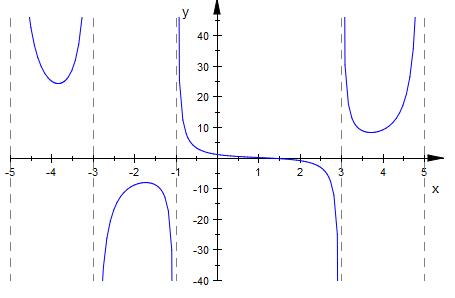
Die Differenzierbarkeit würde die 1.Ableitung betreffen.
ich habe die 1.Ableitung einmal einmal gebildet.
Auch hier wäre für 1 wieder 0 / 0 gegeben.
Aber mir wird es jetzt zu arbeitsaufwendig l´ Hospital
nochmals anzuwenden.
Bei Fragen wieder melden.
mfg Georg