Hallo benötige eure Hilfe bei einer Extremwertaufgabe :)
Also komme bei einer Aufgabe nicht ganz zurecht:(
Gegeben ist die Funktion f mit f(x) = 9 - 0,25x^2 für x ∈ [0;6]
Wählen sie P so,dass das gleichschenklige Dreieck maximalen Flächeninhalt hat.
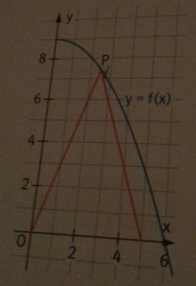
Mein Ansatz : A = 1/2 gh
g = 6-x
h = ?? ( vielleicht y-b)
A(x) = 1/2 (6-x) ((9- 0,25x^2 )-b)
A(x) = 1/2 (6-x) (9+0,25x^2-b)
A(x) = 1/2 (34+1,5x^2-6b-9x-0,25x^3-bx)
und weiter kein plan :(