likeeeeeee22,
auch wenn Deine Frage schon etwas her ist, will ich sie an dieser Stelle beantworten. Vielleicht bringt Dir die Lösung für zukünftige Prüfungsvorbereitungen oder zur Festigung des Lernstoffes etwas.
Ein sinnvoller Ansatz besteht darin, die Lösbarkeitsbedingung für Lineare Gleichungssysteme über die Determinante zu untersuchen. Wir berechnen also von 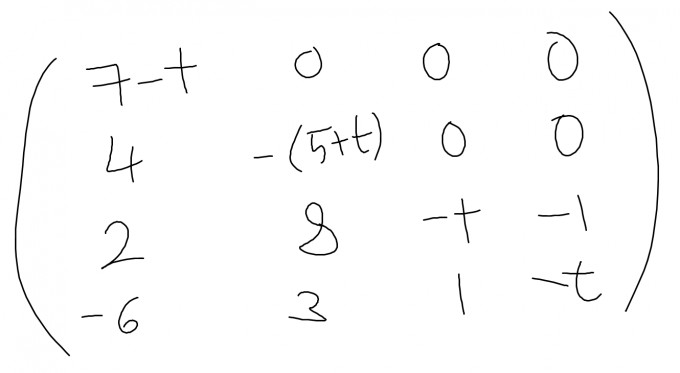
die Determinante. Um Rechenarbeit zu sparen, entwickeln wir sie mithilfe des Laplaceschen Entwicklungssatzes nach der ersten Zeile, da hier 3 Nullen vorhanden sind. Dadurch erhalten wir: 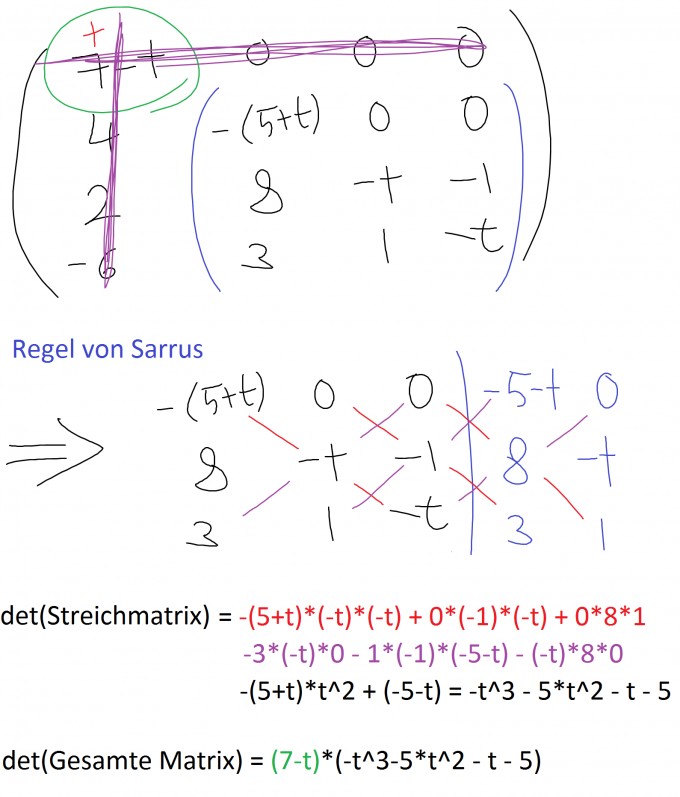
Nun prüfen wir, für welche t die Determinante den Wert 0 annimmt. Dazu lösen wir die Gleichung $$(7-t)\cdot (-t^3-5\cdot t^2-t-5) =0$$ $$\Longleftrightarrow (t-7)\cdot (t+5)\cdot (t^2+1)=0$$ Daraus ergeben sich folgende Lösungen: $$t_1=7$$ $$t_2=-5$$ $$t_3=i$$ $$t_4=-i$$ Es soll t allerdings reell sein, weshalb $$t_3\text{ und } t_4$$ entfallen. Wenn also $$t\in\mathbb{R}\setminus\{-5,7\}$$ ist, dann besitzt das homogene LGS nicht-triviale Lösungen. Du könntest zudem durch Einsetzen der gefundenen t in das LGS prüfen, ob es weitere "nicht-triviale" Lösungen gibt.
André