Hallo rosakatze,
A) Symmetrie heißt das Zauberwort. Alle Dreiecke, die durch den Punkt \(M\) und zwei benachbarten Eckpunkten gebildet werden, sind gleich und gleichschenklig. Ausgehend von der Symmetrieachse die durch \(B\) und \(M\) verläuft, betrachte man zunächst die Dreiecke \(MBC\) und \(MAB\). Beide liegen symmetrisch zur Achse durch \(B\) und \(M\) - so auch die Punkte \(C\) und \(A\). \(C\) ist Spiegelpunkt zu \(A\) und umgekehrt. Und da die Verbindung von Punkt und Bildpunkt immer senkrecht auf der Symmetrieachse steht, steht auch \(AC\) senkrecht auf \(BM\). Mit der gleichen Argumentation kann man zeigen, dass auch \(DE\) senkrecht auf der Verlängerung durch \(BM\) steht.
B) Und da \(AC\) und \(DE\) senkrecht zu \(BM\) verlaufen, sind sie auch parallel. Genauso sind die Strecken \(AE\) und \(BD\) parallel, wenn man die Symmetrieachse durch \(CM\) betrachtet. D.h. bei \(ASDE\) muss es sich mindestens um ein Parallelogramm handeln, und da \(DE=EA\) ist, ist es auch eine Raute.
C) und von der Raute kommt man auch zum Goldenen Schnitt.
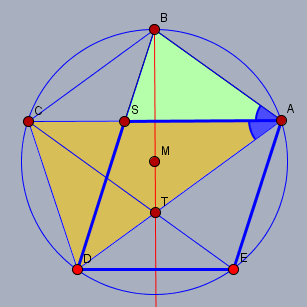
Bei einer Raute sind die Diagonalen auch Winkelhalbierende. Damit sind die Winkel \(EAD\) und \(DAS\)(blau) gleich, und da das Viereck \(ABCT\) auch eine Raute ist, gilt das auch für die beiden eingezeichneten blauen Winkel. Da \(SA=DE=AB\) ist, ist das kleine grüne Dreieck \(ABS\) gleichschenklig. Und da \(C\) und \(D\) symmetrisch zur Verlängerung durch \(AM\) liegen, gilt dies auch für das Dreieck \(ACD\). Zwei gleichschenklige Dreiecke mit gleichem Spitzenwinkel sind kongruent - also alle Streckenverhältnisse sind identisch. Also ist \(SA : SB=DA : CD\) und da \(CD=AB=SA\) ist, sowie \(SB=SC\) (wg. Symmetrie s.o.) , gilt
$$\frac{SA}{SC}=\frac{SA}{SB}=\frac{DA}{CD}=\frac{AC}{SA}=\frac{SC+SA}{SA}$$
somit teilt der Punkt \(S\) die Strecke \(AC\) derart, dass sich der größere Teil \(SA\) zum kleineren Teil \(SC\) genauso verhält, wie die gesamte Strecke \(SC+SA\) zum größeren Teil \(SA\).
C') Mir ist noch ein zweiter hübscher Beweis eingefallen. Dazu spiegelt man das Fünfeck an einer der Diagonalen - hier an \(BE\) und erhält das neue Fünfeck \(A'ED'C'B\).
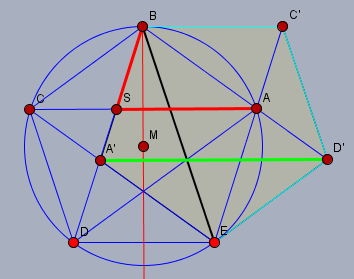
\(A'D'\) verläuft parallel zu \(CA\) - warum das so ist, darfst Du Dir selbst überlegen. Dann zeigt der Strahlensatz, dass \(SB:SA=A'B:A'D'\) ist. Und da \(A'D'=CA\) ist, beweist dies auch, dass \(S\) die Strecke \(CA\) im goldenen Verhältnis teilt.
Falls irgendwelche Fragen sind, so melde Dich bitte.
Gruß Werner