Hallo mala,
fa(x) = -x3 + ax2 - x - ax
a)
Schnittstellen zweier verschiedener Funktionen der Schar:
-x3 + ax2 x - ax = -x3 + bx2 - x - bx | + x3 | + x
ax2 - ax = bx2 - bx | - bx2 | + ax
ax2 - bx2 = ax - bx
(a-b) * x2 = (a-b) * x
x2 = x ⇔ x2 - x = 0 ⇔ x * (x-1) = 0 ⇔ x = 0 oder x = 1
fa(0) = 0 → S1 (0|0)
fa(1) = - 1 + a - 1 + a = - 2 → S2(1| -2)
b)
fa '(x) = - 3·x^2 + 2·a·x - a - 1
fa"(x) = 6x - 2a = 0 ⇔ x = a/3 mit Vorzeichenwechsel von fa"(x)
fa( a/3) ) = 2·a3/27 - a2/3 - a/3 → Wendepunkte Wa( a/3 | 2·a3/27 - a2/3 - a/3 )
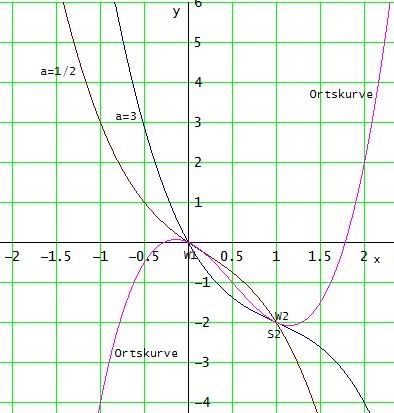
Ortskurve
x = a/3 → a = 3x
y = 2·a3/27 - a2/3 - a/3 = 2·x3 - 3·x2 - x
Gruß Wolfgang