Sagen wir wir wollen die Wahrscheinlichkeit für \(P(56≤X≤45)\) mit einem Erwartungswert von \(56\) und einer Standardabweichung von \(8\) berechnen. Das tun wir dann wie folgt:$$\int_{45}^{56}\frac{1}{\sqrt{2\pi\cdot 8^2}}\cdot e^{-\frac{(x-56)^2}{2\cdot8^2 }}dx ≈ 0.4154342776 $$
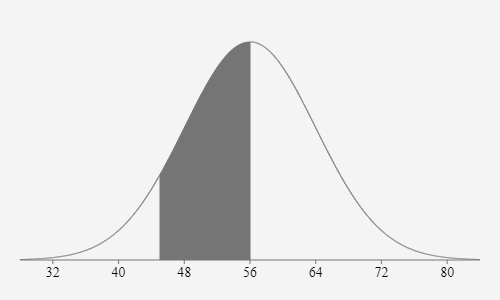
Für Wahrscheinlichkeit mit \(P(X≤64)\). Dann berechnest du:$$\int_{-\infty}^{64}\frac{1}{\sqrt{2\pi\cdot 8^2}}\cdot e^{-\frac{(x-56)^2}{2\cdot8^2 }}dx ≈ 0.841345$$ Oder auch die Wahrscheinlichkeit für \(P(X≥64)\)$$\int_{64}^{\infty}\frac{1}{\sqrt{2\pi\cdot 8^2}}\cdot e^{-\frac{(x-56)^2}{2\cdot8^2 }}dx ≈ 0.158655$$