Aufgabe:
$$ U:=\left( \begin{array}{r}{2} \\ {5} \\ {9}\end{array}\right), \left( \begin{array}{r}{0} \\ {-1} \\ {-3}\end{array}\right) W:=\left( \begin{array}{r}{-3} \\ {1} \\ {6}\end{array}\right), \left( \begin{array}{l}{5} \\ {3} \\ {0}\end{array}\right) $$
$$ \text{U und W sind Unterräume des }\mathbb{R}^{3} . \text { Bestimmen Sie eine Basis des Raumes } U \cap W \subseteq \mathbb{R}^{3} ! $$
Problem/Ansatz:
Ich habe mich wohl verrechnet, weiß aber nicht wo, fällt euch was auf ?
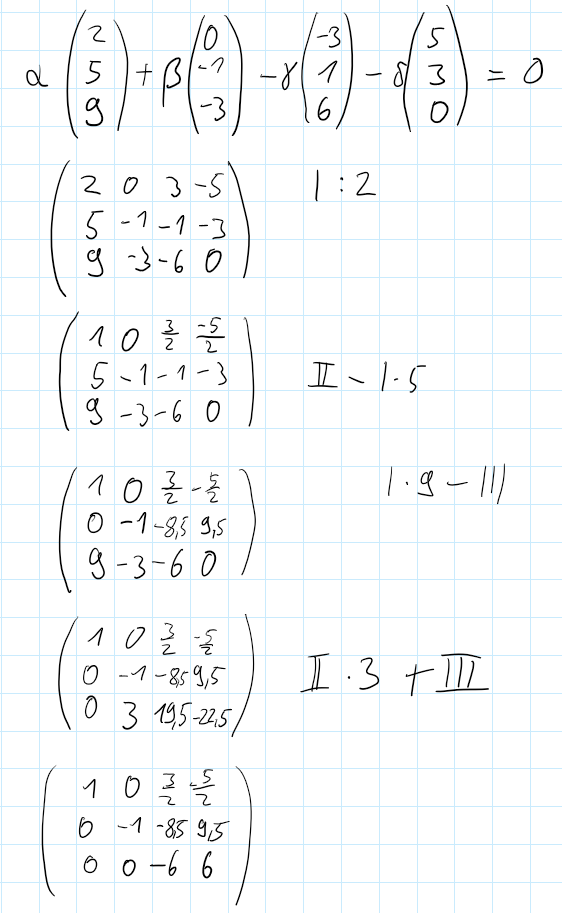
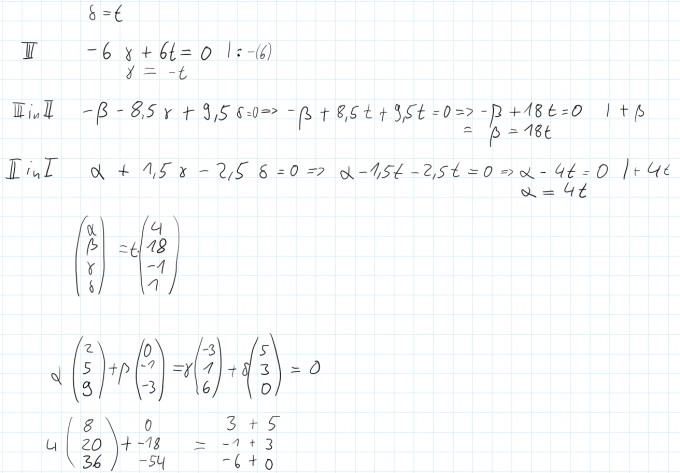
Am Ende müsste ja das gleiche raus kommen. Allerdings ist -18 ≠ -6 also müsste ja γ= -3 sein. Dann geht der Rest aber nicht...