folgende Aufgaben (Ein Teil habe ich bereits hinbekommen):
$$ \begin{array}{l}{\text {Gegeben sei die Matrix } A=\left(\begin{array}{cc}{-3} & {4} \\ {2} & {-1}\end{array}\right) \text { und eine lineare Abbildung } \varphi : \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \text { mit }} \\ {x \mapsto \varphi(x)=A x} \\ {\text { a) Vektoren } x \in \mathbb{R}^{2} \text { werden in der } x_{1}-x_{2}-\text { Ebene durch Punkte dargestellt. Durch }}\\{x_{1} \in\{-2,-1,0,1,2\}, x_{2} \in\{-2,-1,0,1,2\}, x=\left(\begin{array}{c}{x_{1}} \\ {x_{2}}\end{array}\right) \in\{-2,-1,0,1,2\} \times\{-2,-1,0,1,2\} \text { wird ein Punkt- }} \\ {\text { raster von } 5 \times 5 \text { Punkten definiert. Stelle Sie alle so definierten Vektoren } x \text { in einem }} \\ {\text { kartesischen } x_{1}-x_{2}-\text { Koordinatensystem (Originalebene) und alle Bilder } y=\varphi(x)} \\ {\text { dieser Vektoren in einem zweiten kartesischen Koordinatensystem (Bildebene) dar! }} \\ {\text { Verwenden Sie für beide Koordinatensysteme die gleiche Achsenteilung! }} \\{\text { b) Ermitteln Sie die Determinante von } A \text { sowie das charakteristische Polynom von } A} \\ {\text { indem Sie die Determinante } \chi_{A}(t)=\operatorname{det}(A |-t \cdot E) \text { berechnen! }} \\ {\text { c) Berechnen Sie die Eigenwerte von } A !}\end{array} $$
$$ \begin{array}{l}{\text { d) Zeichnen Sie in die Originalebene die Gerade durch den Ursprung und den Vektor }} \\ {\qquad v_{1}=\left(\begin{array}{c}{-2} \\ {1}\end{array}\right) \text { sowie in die Bildebene das Bild dieser Geraden ein! Sie stellen fest: }} \\ {\text { Original-und Bildgerade haben die gleiche Richtung. }} \\ {\text { Messen Sie die Länge des Vektors } v_{1} \text { und seines Bildes } \varphi\left(v_{1}\right) ; \text { stellen Sie eine }} \\ {\text { Verbindung zu den Eigenwerten her! }}\end{array} $$ $$ \begin{array}{l}{\text { e) Gibt es eine zweite Gerade mit der in d) vorliegenden Eigenschaft? Wenn ja, geben }} \\ {\text { Sie zwei Punkte auf dieser Geraden an! }}\end{array} $$
Fragen:
Was hat es mit der linearen Abbildung auf sich? Ich verstehe die Notation nicht.
zu a) Ich würde es so verstehen(nur eben dann mit noch mehr Punkten, dann entsteht ja so ein Muster: 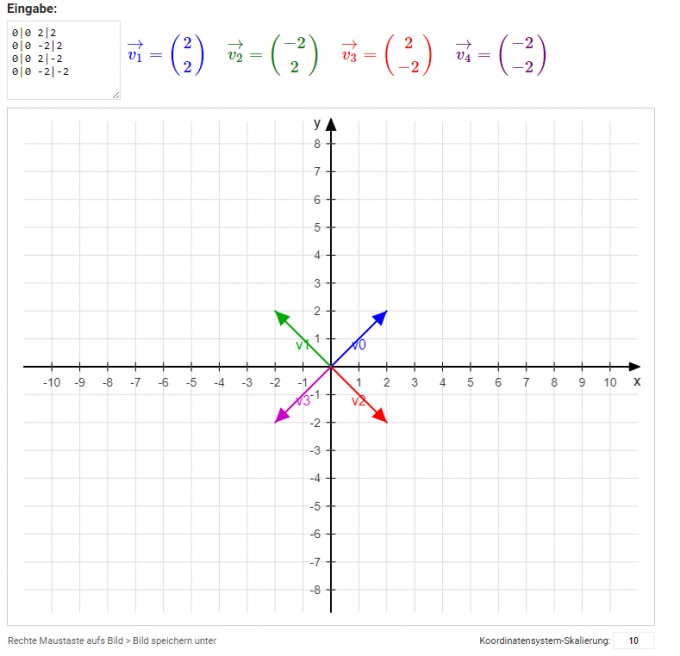
Was ist dann aber weiter mit den Bildern gemeint? Und x1 ,x2 ist doch eigentlich wie x und y, oder?
Bei b)/c) bin ich auf x2 +4x-5 gekommen und auf die Eigenwerte {-5, 1}
LG und hoffentlich angenehmen Tag