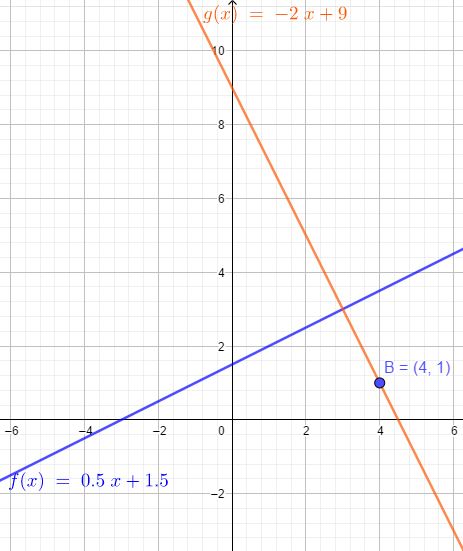
wenn auf einer Geraden mit der Steigung m eine andere Gerade senkrecht steht, so hat diese die Steigung -\( \frac{1}{m} \) (= negativer Kehrwert).
Deine Gerade hat die Steigung 0,5 = \( \frac{1}{2} \) , -\( \frac{1}{m} \) ist dann -2.
Wir können also schreiben
g(x) = -2x + b
b berechnest du, indem du die Koordinaten des Punktes B für y bzw. g(x) und x einsetzt:
1= -2*4 + b
und nach b auflöst.
Falls du dazu noch Fragen hast, melde dich.
Gruß, Silvia