... und ich wundere mich, dass Du das vorher nicht wusstest ;-) aber es geht anderen genauso. Schau Dir mal folgende Skizze an. Dort habe ich eine Gerade \(g\) eingezeichnet.
(klick auf das Bild)
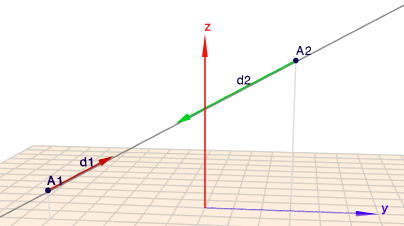
Die Gerade \(g\) hat die Gleichung(en) $$g: \quad \vec x = \begin{pmatrix}2\\ -5\\ 1\end{pmatrix} + t \begin{pmatrix}-1\\ 2\\ 1\end{pmatrix} = \begin{pmatrix}-2\\ 3\\ 5\end{pmatrix} + r \begin{pmatrix}2\\ -4\\ -2\end{pmatrix}$$siehst Du, dass es sich um die identische Gerade \(g\) handelt? In der Zeichnung sieht man es natürlich gleich, \(A_1\) und der rote Vektor sind die linke Form und \(A_2\) mit dem grünen Vektor ist die rechte. Aber in der Rechnung ist die Identität nicht so offensichtlich. Setzt man für \(r=2 - \frac t2\) kann man die rechte Form in die linke überführen.
Schaue es Dir an, rechne es nach und denke drüber nach. Wenn Du die Punkt-Richtungs-Form der Geraden wirklich verstanden hast, muss Dir das niemand mehr erklären ;-)
PS.: im Bild habe ich die Gerade leicht versetzt gezeichnet, damit man die Vektoren besser sieht.