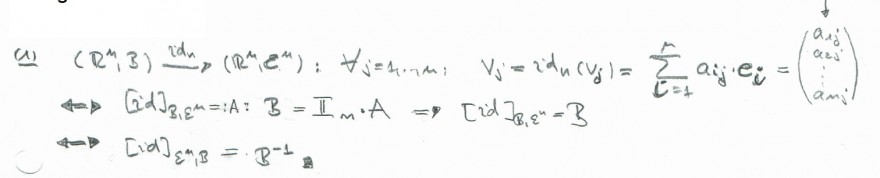Aufgabe:
Was ist die Identität einer Matrix?
Ich habe folgende Aufgabe:
1. Sei \( \mathcal{B}=\left(\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\right) \) eine beliebige Basis des \( \mathbb{R}^{n}, \) und sei \( \mathcal{E}^{n}=\left(\mathbf{e}_{1}, \ldots, \mathbf{e}_{n}\right) \)
die Standardbasis. Wie sieht die Übergangsmatrix \( P \) von \( \mathcal{B} \) zu \( \mathcal{E}^{n} \) aus? Wie können Sie die Übergangsmatrix von \( \mathcal{E}^{n} \) zu \( \mathcal{B} \) bestimmen?
Problem/Ansatz:
Hier muss ich ja eigentlich die Einheitsmatrix zu umstellen mit dem Gauss-Jordan-Verfahren, dass ich dann genau B bekomme. Und das wäre ja eigentlich B^-1 , da B* B^-1 = In ergibt. In den Lösungen steht folgendes, ich weiss aber nicht, was id ist und was es genau beschreiben sollte, kann mir das jemand erklären: