Aufgabe:
Ich soll die beiden Integrale über ihre Stammfunktionen berechnen und anschließend die Integrale als Flachenstücke interpretieren und geometrisch zeigen, warum ihre Summe 1 ist.
Text erkannt:
\( \int \limits_{0}^{1} x^{2} \mathrm{~d} x+\int \limits_{0}^{1} \sqrt{x} \mathrm{~d} x=1 \)
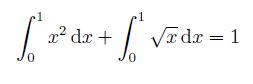
Problem/Ansatz:
Ich hatte Integrale leider nur sehr oberflächlich in der Schule und weiß nicht genau, wie ich an diese Aufgabe herangehen soll. Ich würde mich freuen, wenn mir da jemand weiterhelfen könnte! :)
Text erkannt:
\( \int \limits_{0}^{1} x^{2} \mathrm{~d} x+\int \limits_{0}^{1} \sqrt{x} \mathrm{~d} x=1 \)