Hallo,
zu a) ich gehe davon aus, dass die Achse \(a\) die Menge der Fixpunkte der Scherung sein soll. Damit ist allerdings die Angabe \(P,\,P',\,a\) nicht mehr unabhängig, da die Gerade durch \(PP'\) zwingend parallel zu \(a\) verlaufen muss. Es würde reichen, ein Punktepaar \(P,\,P'\) anzugeben und einen Fixpunkt \(F \not\in g(P,P')\). Die Achse \(a\) ist dann definiert als die Gerade durch \(F\), die parallel zu \(g(P,P')\) verläuft.
Aber egal. Ich glaube ein Bild sagt mehr als viele Worte:
https://jsfiddle.net/WernerSalomon/578qzxrm/26/
Du kannst oben die Punkte \(A\), \(B\), \(C\), \(P\) und \(P'\) mit der Maus verschieben und dann siehst Du jeweils was für ein Effekt sich damit ergibt.
Am Beispiel des Punktes \(A\) kann an sehen, wie Scherung 'funktioniert'. Die Gerade durch \(PA\) (blau) schneidet \(a\) (lila) in \(F_a\). Und der gescherte Punkt \(A'\) ist der Schnittpunkt der Geraden durch \(P'F_a\) (blau) mit der Parallelen durch \(A\) (grau) zur Achse \(a\).
Und damit ist die Scherung auch eindeutig definiert.
Bem.: bei Punkten, die auf der Parallelen durch \(P\) zu \(a\) liegen, wählt man ggf. eine alternative Konstruktion. Aber es ändert sich am Prinzip nichts,
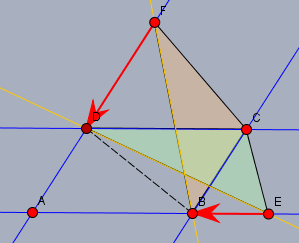
zu b) durch Scherung kann man das Dreieck \(\triangle BCF\) in das flächengleiche Dreieck \(\triangle BCD\) überführen. Ebenso durch Scherung lässt sich das Dreieck \(\triangle CDE\) in das flächengleiche Dreieck \(\triangle BCD\) überführen. Also haben die beiden Dreiecke \(\triangle BCF\) und \(\triangle CDE\) den gleichen Flächeninhalt.
Das Bild zur Aufgabe
Gruß Werner