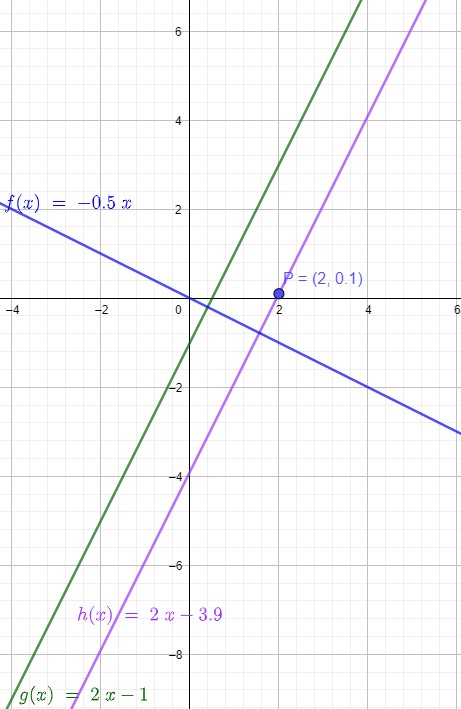
Hallo,
paralle Geraden haben die gleiche Steigung m, hier = 2
Allgemeine Geradengleichung y = mx + n
Setze die Koordinaten dieses Punktes in die Geradengleichung ein, um n zu bestimmen. Damit hast du die Gleichung von h.
Schnittpunkt der Geraden mit der y-Achse: Setze 0 für x in die Gleichung ein und rechne aus.
Für die Steigung senkrecht aufeinander stehender Geraden gilt: \(m_1\cdot m_2=-1\)
Oder anders ausgedrückt: die Steigung der Senkrechten ist der negative Kehrwert der Geraden, das wäre hier dann \( -\frac{1}{2} \) .
Da die Gerade durch den Ursprung verläuft, der Schnittpunkt mit der y-Achse bei x = 0 ist, gibt es kein n.
Gruß, Silvia