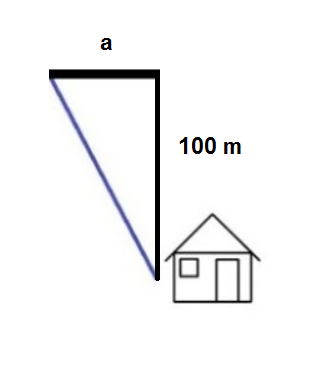
Anstatt die Kosten zu minimieren, kann man auch das Kostenersparnis maximieren. Es gibt Leute, die sagen dem "das duale Problem". Dazu wird nur das rechtwinklige Dreieck rechts in der Skizze benötigt. Das Ersparnis ist gleich die Kosten der vermiedenen Strecke (Katheten) minus die Kosten der gebauten Strecke (Hypotenuse).
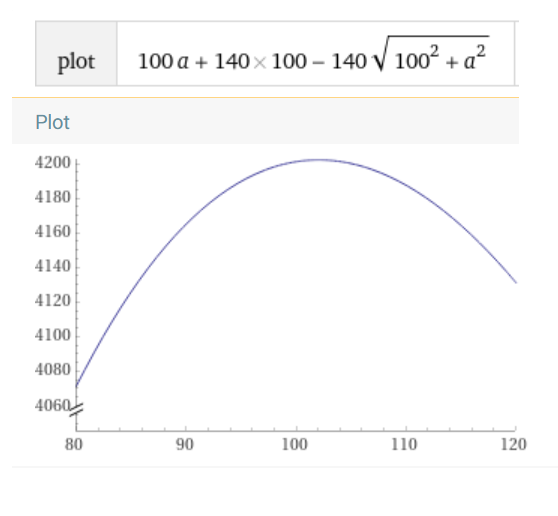
Ersparnis (a) = 100a + 140*100 - 140\( \sqrt{100^2 + a^2} \)
\( \frac{\partial}{\partial a}\left(100a+140\cdot100-140\sqrt{100^{2}+a^{2}}\right)=100-\Large\frac{140a}{\sqrt{a^{2}+10000}}\normalsize = 0 \)
⇒ \(a = \Large \frac{125 \sqrt{6}}{3} \)