Aufgabe:
Das Polynom p x = 2 x3 6 x 4 ist vom Grad 3 und besitzt den Leit-Koeffizienten a3 = 2 .
Seinen Graphen koennen wir qualitativ skizzieren, wenn wir fuer p x eine Faktor-Zerlegung
angeben. Es gilt:
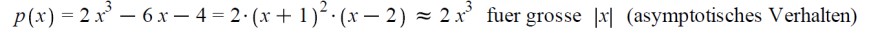
Text erkannt:
\( p(x)=2 x^{3}-6 x-4=2 \cdot(x+1)^{2} \cdot(x-2) \approx 2 x^{3} \) fuer grosse \( |x| \) (asymptotisches Verhalten)
In dieser Darstellung ist der Zahlen-Faktor 2 der Leit-Koeffizient. Der Linear-Faktor x 1
besitzt die Vielfachheit 2 . Wir sprechen von einer doppelten Nullstelle x1 = x2 = 1. Zum Linear-
Faktor x 2 gehoert die Vielfachheit 1 , also die einfache Nullstelle x3 = 2 . Mehrfache
Nullstellen sind analog definiert.
Wir diskutieren nun den Einfluss der Vielfachheit einer Nullstelle auf das lokale Verhalten des
Graphen von p x in der Naehe dieser Nullstelle.
Text erkannt:
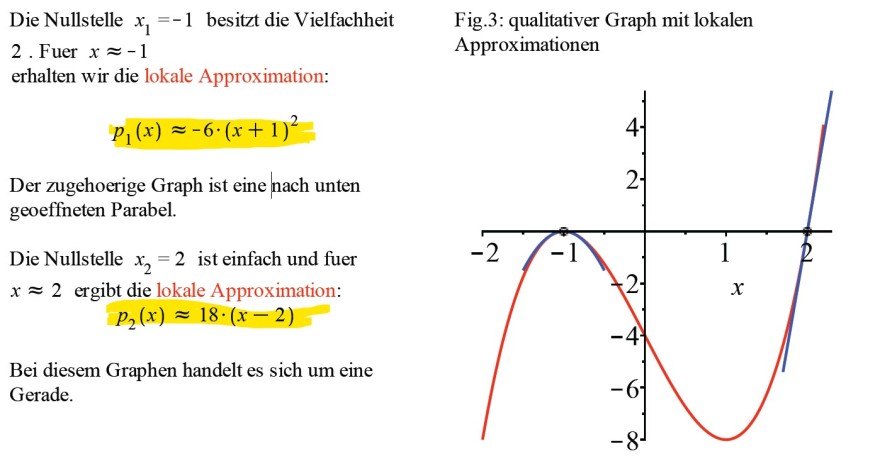
Die Nullstelle \( x_{1}=-1 \) besitzt die Vielfachheit Fig.3: qualitativer Graph mit lokalen
2 . Fuer \( x \approx-1 \)
Approximationen
erhalten wir die lokale Approximation:
Copyright -> ZHAW, Schweiz Analysis 1 (Informatik)
Problem/Ansatz
Ich verstehe, wie die Funktion entstehen und wie ich mit dem Graphen den Funktionsparameter erstellen kann, jedoch stellt sich mir die Frage, wie ich auf die -6 und -18 komme.
Ich denke das es einen einfachen Grund hat, jedoch habe ich dieses Skript im Internet gefunden für die eigenständige Vorbereitung auf das erste Semester und konnte noch keine Vorlesung besuchen.
