Aufgabe:
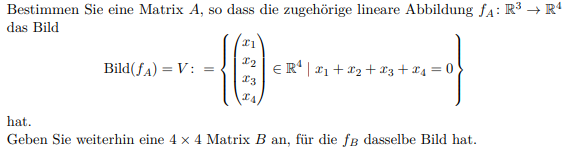
Text erkannt:
Bestimmen Sie eine Matrix \( A \), so dass die zugehörige lineare Abbildung \( f_{A}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{4} \) das Bild
\( \operatorname{Bild}\left(f_{A}\right)=V:=\left\{\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{array}\right) \in \mathbb{R}^{4} \mid x_{1}+x_{2}+x_{3}+x_{4}=0\right\} \)
hat.
Geben Sie weiterhin eine \( 4 \times 4 \) Matrix \( B \) an, für die \( f_{B} \) dasselbe Bild hat.
Problem/Ansatz:
Hallo, ich brauche Hilfe bei dieser Aufgabe, mein Ansatz ist: das Matrix Bildungsverfahren wo man anand einer Matrix ein Bild berechnet einfach anderes herum zu machen und die schritte wie: Transponieren, zeilensufenform usw. in anderer reinfolge zu machen bis man die Matrix hat. Kann mir jemand sagen, ob dies so richtig ist und falls nicht, erklären wie es dann geht bzw. Rechenbeispiele bringen. Ebenfalls bei dem zweiten teil bin ich sehr überfordert "4x4 Matrix B an, für fB dasselbe Bild hat"
LG