Aufgabe:

Text erkannt:
\( \underline{\mathrm{B}}=\left(e_{1}, e_{2}\right) \) die geordnete Standardbasis von \( V \) sowie
\( \underline{\mathrm{C}}:=\left(\left(\begin{array}{l} 1 \\ 2 \end{array}\right),\left(\begin{array}{c} 0 \\ -1 \end{array}\right)\right) \text { und } \underline{\mathrm{D}}:=\left(\left(\begin{array}{l} 1 \\ 1 \end{array}\right),\left(\begin{array}{l} 3 \\ 2 \end{array}\right)\right) \text {. } \)
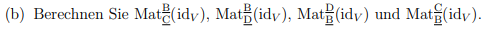
Text erkannt:
(b) Berechnen Sie Mat \( \frac{\underline{\mathrm{C}}}{}\left(\mathrm{id}_{V}\right), \operatorname{Mat}_{\underline{\underline{D}}}\left(\mathrm{id}_{V}\right) \), Mat \( _{\underline{\underline{\mathrm{B}}}}\left(\mathrm{id}_{V}\right) \) und Mat \( \frac{\underline{\mathrm{C}}}{\underline{\mathrm{D}}}\left(\mathrm{id}_{V}\right) \).
Problem/Ansatz:
ich habs gegooglet und ich hab in den Vorlesungen geschaut aber ich habe mir keine logische Standardbasis gefunden.
ich habe für B raus
dass 1 2
-1 -1
ist