Betrachten Sie die Funktionenschar zu \( f_{k}(x)=\left(1-k x^{2}\right) e^{x} \)
a) Es sind folgende zwei Graphen dieser Schar abgebildet. Bestimmen Sie die Parameterwerte.
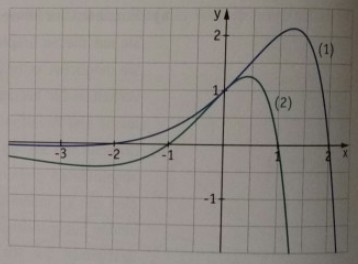
b) Untersuchen Sie, ob alle Graphen dieser Schar prinzipiell diesen Verlauf haben. Begründen Sie Ihre Antwort möglichst allgemein.
c) Untersuchen Sie, ob verschiedene Graphen dieser Schar gemeinsame Punkte haben können.
d) An der Stelle 0 liegt eine weitere Besonderheit aller Graphen der Schar vor. Nennen und begründen Sie diese.
e) Zeigen Sie, dass \( F_{k}(x)=\left(-k x^{2}+2 k x-2 k+1\right) e^{x} \) eine Stammfunktion zu \( f_{k} \) ist. Dokumentieren Sie einen Lösungsweg, đer auch ohne Einsatz von Technologie nachvollziehbar ist.
f) Bestimmen Sie den Flächeninhalt der Fläche, die der Graph zu \( \mathrm{f}_{\mathrm{k}} \) für \( \mathrm{k}>0 \) mit der \( x \)-Achse einschließt.