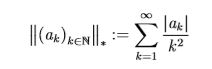Hallo liebe Leute,
ich hänge mal wieder bei einer Aufgabe. Ich hab als Vektorraum den Raum der beschränkten Folgen gegeben. Und als Norm die Reihe unten. Jetzt soll ich eine Cauchy-Folge konstruieren, die nicht in V konvergiert und dabei tu ich mich schwer.
Eine Idee wäre, ich setze als Grenzwert dieser Folge eine unbeschränkte Folge c_n. Diese Folge muss eingesetzt in die "Norm < oo" erfüllen. Und dann definier ich mir halt: v_n = (c_1, c_2, c_3, ..., c_n, 0, 0, 0...) als eine Folge in dieser Folge (wobei n bei v dasselbe n ist wie bei c)
Dann wäre meine Cauchy-Folge: (x_n) = (v_1, v_2, v_3,....) ohne Grenzwert in V. Soweit die Idee, die Frage ist ob ich so eine Folge überhaupt wählen kann. Besonders Bauchweh macht mir die Bedingung: "Diese Folge muss eingesetzt in die "Norm < oo" erfüllen", da sie sonst irgendwann nicht beschränkt wäre oder?
Mit der Bitte um Gedanken,
Mathstîger